pymnet.lcc_brodka¶

pymnet.lcc_brodka(net, node, anet=None, threshold=1, undefReturn=0.0)¶

The “cross-layer clustering coefficient” defined by Brodka et al.

The clustering coefficient for node 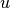$u$ is given by the formula (see Ref. [2]):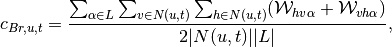

$c_{Br,u,t} = \frac{\sum_{\alpha \in L} \sum_{v \in N(u,t)} \sum_{h \in N(u,t)}( \mathcal{W}_{hv\alpha} + \mathcal{W}_{vh\alpha})}{2 |N(u,t)| |L|},$

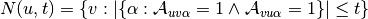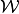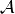where $N(u,t) = \{ v : | \{\alpha : \mathcal{A}_{uv\alpha}=1 \wedge \mathcal{A}_{vu\alpha}=1 \}| \leq t \}$ is the set of layers, $\mathcal{W}$ is the rank-3 weighted adjacency tensor of the multiplex network, and $\mathcal{A}$ is the rank-3 unweighted adjacency tensor of the multiplex network.

One can get the “multi-layered clustering coefficient in extendend neighborhood” by setting the threshold to one 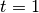$t=1$ , and the “multi-layered clustering coefficient in reduced neighborhood” by setting the threshold to the total number of layers $t=|L|$ .

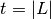Parameters

netMultiplexNetwork with aspects=1: The input network.
nodeany object: The focal node. Given as the node index in the network.
anetMultilayerNetwork with aspects=0: The aggregated network. If given, it is used to speed up the calculation. NOTE: for undirected networks the “normal” aggregation strategy (produced for example by the aggregate function in this library) is suitable, but for directed networks the network needs to be aggregated such that thresholding it will produce the neighborhood sets $N(u,t)$ .
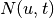thresholdint, string: Threshold for number of layers, see Ref. [2]. If ‘all’, then the threshold is the total number of layers.

Returns

float or object: The clustering coefficient value.