Overview¶
The data types in this library follow the mathematical definitions of various multilayer network types defined in the article “Multilayer Networks”, M. Kivela et al., arXiv:1309.7233 [physics.soc-ph]. In the article a multilayer network is defined as a general mathematical structure and all the other types of networks are defined as special cases of that structure. Here we take e a similar approach and define a class MultilayerNetwork such that it represents the mathematical definition of the multilayer network. All the other network classes then inherit the MultilayerNetwork class. Currently we have the MultiplexNetwork class which represent multiplex networks as defined in the article. In the article there were several constraints defined for multiplex networks. Some of these constraints, such as “categorical” and “ordinal” couplings, are also implemented in this library. Instances of MultiplexNetwork that are constrained in this way can be implemented efficiently and the algorithms dealing with general multilayer networks can take advantage of the information that the network object is constrained.
Computational efficiency¶
One often wants to study large scale synthetic networks or big network data sets. In this type of situations the most important thing is to consider how the memory and time requirements of the data structures and the algorithms scale with the size of the network. This library is designed with these scaling requirements in mind. The average scaling in time and memory should typically be optimal for number of nodes, 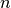 , number of layers,
, number of layers, 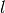 , and number of edges,
, and number of edges,  . We typically consider that the number of aspects,
. We typically consider that the number of aspects,  , to be constant and not dependent on the size of the data. Note, however, that the current implementation is only in Python (the C++ version implementation is in the planning phase), and thus the constant factor in the memory and time consumption is typically fairly large.
, to be constant and not dependent on the size of the data. Note, however, that the current implementation is only in Python (the C++ version implementation is in the planning phase), and thus the constant factor in the memory and time consumption is typically fairly large.
The main data structure underlying the general multilayer network representation is a global graph 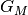 implemented as dictionary of dictionaries. That is, the graph is a dictionary where for each node, e.g.
implemented as dictionary of dictionaries. That is, the graph is a dictionary where for each node, e.g. 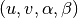 , is a key and values is another dictionary containing information about the neighbors of each node. Thus, the inner dictionaries have the neighboring nodes as keys and weigths of the edges connecting them as values. This type of structure ensures that the average time complexity of adding new nodes, removing nodes, querying for exitense of edges, or their weights, are all on average constant, and iterating over the neighbors of a node is linear. Further, the memory requirements in scale as
, is a key and values is another dictionary containing information about the neighbors of each node. Thus, the inner dictionaries have the neighboring nodes as keys and weigths of the edges connecting them as values. This type of structure ensures that the average time complexity of adding new nodes, removing nodes, querying for exitense of edges, or their weights, are all on average constant, and iterating over the neighbors of a node is linear. Further, the memory requirements in scale as 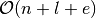 , and are typically dominated by the number of edges in the network.
, and are typically dominated by the number of edges in the network.
Multiplex networks are a special case of multilayer networks, and we could easily employ the same data structure as for the multilayer networks. There are few reason why we don’t want to do that here. First, in multiplex networks we typically want to iterate over intra-layer links of a node in a single layer, and this would require one to go through all the inter-layer edges too if the multilayer network data structure was used. Second, in most cases we don’t want to explicitely store all the inter-layer links. For example, when we have a multiplex network with categorical couplings which are of equal weight the number of inter-layer edges grows as 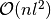 . In the multiplex network data structure in this library we only always store the intra-layer networks separately, and don’t store the inter-layer edges explicitely but only generate them according to given rules when they are needed. This ensures that we can always iterate over the intra-layer edges in time which is linear to their number, and that having the inter-layer edges only requires constant memory (i.e. the memory to store the rule to generate them).
. In the multiplex network data structure in this library we only always store the intra-layer networks separately, and don’t store the inter-layer edges explicitely but only generate them according to given rules when they are needed. This ensures that we can always iterate over the intra-layer edges in time which is linear to their number, and that having the inter-layer edges only requires constant memory (i.e. the memory to store the rule to generate them).
Examples¶
Next we give few examples of simple tasks and the time it takes to complete them in a normal desktop computer. This is simply to give an idea about the practical efficiency of the library and computation times of typical jobs. All the runs using PyPy 2.1 and desktop computer with AMD Phenom II X3 processor and 2 GB of memory running Linux.
Multiplex ER network with large number of layers¶
First, we create an Erdos-Renyi multiplex network with small number of nodes and large number of layers and categorical couplings. We choose to have 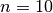 nodes and
nodes and 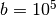 layers with edge probability of
layers with edge probability of 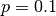 . This will result in a network with around
. This will result in a network with around 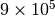 intra-layer edges and
intra-layer edges and 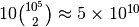 inter-layer edges. The command for creating this network is
inter-layer edges. The command for creating this network is
>>> net=er(10,10**5*[0.1])
The command takes around 2.4 seconds to run (averaged over 100 runs) in the above mentioned computer. Note that, internally, this command creates a sparse matrix representation of the intra-layer networks (i.e. only edges that exist are created) and the inter-layer edges are not actually created explicitely. Creating a full adjacency tensor, or a supra-adjacency matrix, would require creating an object with 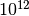 elements, and even a sparse representation with all edges explicitely generated would have around
elements, and even a sparse representation with all edges explicitely generated would have around 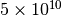 elements.
elements.
Multiplex ER network with large number of nodes¶
Next we create an ER network with 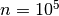 nodes,
nodes, 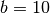 layers, and average degree around one. The total number of intra-layer edges will be around
layers, and average degree around one. The total number of intra-layer edges will be around 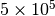 . This can be done with the following command
. This can be done with the following command
>>> net=er(10**5,10*[10**-5])
The total time to complete this task is around 3.4 seconds.