Author Archives: bolozna

M. Kivelä, S. Arnaud-Haond, J. Saramäki

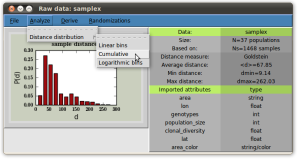
The recent application of graph-based network theory analysis to biogeography, community ecology and population genetics has created a need for user-friendly software, which would allow a wider accessibility to and adaptation of these methods. EDENetworks aims to fill this void by providing an easy-to-use interface for the whole analysis pipeline of ecological and evolutionary networks starting from matrices of species distributions, genotypes, bacterial OTUs or populations characterized genetically. The user can choose between several different ecological distance metrics, such as Bray-Curtis or Sorensen distance, or population genetic metrics such as FST or Goldstein distances, to turn the raw data into a distance/dissimilarity matrix. This matrix is then transformed into a network by manual or automatic thresholding based on percolation theory or by building the minimum spanning tree. The networks can be visualized along with auxiliary data and analysed with various metrics such as degree, clustering coefficient, assortativity and betweenness centrality. The statistical significance of the results can be estimated either by resampling the original biological data or by null models based on permutations of the data.

Molecular Ecology Resources 15(1) p. 117–122

Read the full text

The related software

M. Kivelä, A. Arenas, M. Barthelemy, J. P. Gleeson, Y. Moreno, M. A. Porter

In most natural and engineered systems, a set of entities interact with each other in complicated patterns that can encompass multiple types of relationships, change in time and include other types of complications. Such systems include multiple subsystems and layers of connectivity, and it is important to take such ‘multilayer’ features into account to try to improve our understanding of complex systems. Consequently, it is necessary to generalize ‘traditional’ network theory by developing (and validating) a framework and associated tools to study multilayer systems in a comprehensive fashion. The origins of such efforts date back several decades and arose in multiple disciplines, and now the study of multilayer networks has become one of the most important directions in network science. In this paper, we discuss the history of multilayer networks (and related concepts) and review the exploding body of work on such networks. To unify the disparate terminology in the large body of recent work, we discuss a general framework for multilayer networks, construct a dictionary of terminology to relate the numerous existing concepts to each other and provide a thorough discussion that compares, contrasts and translates between related notions such as multilayer networks, multiplex networks, interdependent networks, networks of networks and many others. We also survey and discuss existing data sets that can be represented as multilayer networks. We review attempts to generalize single-layer-network diagnostics to multilayer networks. We also discuss the rapidly expanding research on multilayer-network models and notions like community structure, connected components, tensor decompositions and various types of dynamical processes on multilayer networks. We conclude with a summary and an outlook.

Journal of Complex Networks 2(3), p. 203-271

Read the full text

M. De Domenico, A. Solé-Ribalta, E. Cozzo, M. Kivelä, Y. Moreno, M. A. Porter, S. Gómez, A. Arenas

A network representation is useful for describing the structure of a large variety of complex systems. However, most real and engineered systems have multiple subsystems and layers of connectivity, and the data produced by such systems are very rich. Achieving a deep understanding of such systems necessitates generalizing “traditional” network theory, and the newfound deluge of data now makes it possible to test increasingly general frameworks for the study of networks. In particular, although adjacency matrices are useful to describe traditional single-layer networks, such a representation is insufficient for the analysis and description of multiplex and time-dependent networks. One must therefore develop a more general mathematical framework to cope with the challenges posed by multilayer complex systems. In this paper, we introduce a tensorial framework to study multilayer networks, and we discuss the generalization of several important network descriptors and dynamical processes—including degree centrality, clustering coefficients, eigenvector centrality, modularity, von Neumann entropy, and diffusion—for this framework. We examine the impact of different choices in constructing these generalizations, and we illustrate how to obtain known results for the special cases of single-layer and multiplex networks. Our tensorial approach will be helpful for tackling pressing problems in multilayer complex systems, such as inferring who is influencing whom (and by which media) in multichannel social networks and developing routing techniques for multimodal transportation systems.

Phys. Rev. X 3, 041022

Read the full text

R. Toivonen, M. Kivelä, J. Saramäki, M. Viinikainen, M. Vanhatalo, M. Sams

The aim of this work was to study the similarity network and hierarchical clustering of Finnish emotion concepts. Native speakers of Finnish evaluated similarity between the 50 most frequently used Finnish words describing emotional experiences. We hypothesized that methods developed within network theory, such as identifying clusters and specific local network structures, can reveal structures that would be difficult to discover using traditional methods such as multidimensional scaling (MDS) and ordinary cluster analysis. The concepts divided into three main clusters, which can be described as negative, positive, and surprise. Negative and positive clusters divided further into meaningful sub-clusters, corresponding to those found in previous studies. Importantly, this method allowed the same concept to be a member in more than one cluster. Our results suggest that studying particular network structures that do not fit into a low-dimensional description can shed additional light on why subjects evaluate certain concepts as similar. To encourage the use of network methods in analyzing similarity data, we provide the analysis software for free use (http://www.becs.tkk.fi/similaritynets/).

PloS ONE 7(1): e28883

Read the full text

M. Kivelä, R. K. Pan, K. Kaski, J. Kertész, J. Saramäki, M. Karsai

In temporal networks, both the topology of the underlying network and the timings of interaction events can be crucial in determining how a dynamic process mediated by the network unfolds. We have explored the limiting case of the speed of spreading in the SI model, set up such that an event between an infectious and a susceptible individual always transmits the infection. The speed of this process sets an upper bound for the speed of any dynamic process that is mediated through the interaction events of the network. With the help of temporal networks derived from large-scale time-stamped data on mobile phone calls, we extend earlier results that indicate the slowing-down effects of burstiness and temporal inhomogeneities. In such networks, links are not permanently active, but dynamic processes are mediated by recurrent events taking place on the links at specific points in time. We perform a multiscale analysis and pinpoint the importance of the timings of event sequences on individual links, their correlations with neighboring sequences, and the temporal pathways taken by the network-scale spreading process. This is achieved by studying empirically and analytically different characteristic relay times of links, relevant to the respective scales, and a set of temporal reference models that allow for removing selected time-domain correlations one by one. Our analysis shows that for the spreading velocity, time-domain inhomogeneities are as important as the network topology, which indicates the need to take time-domain information into account when studying spreading dynamics. In particular, results for the different characteristic relay times underline the importance of the burstiness of individual links.

Journal of Statistical Mechanics P03005

Read the full text

R. K. Pan, M. Kivelä, J. Saramäki, K. Kaski, J. Kertész

We apply a variant of the explosive percolation procedure to large real-world networks and show with finite-size scaling that the university class, ordinary or explosive, of the resulting percolation transition depends on the structural properties of the network, as well as the number of unoccupied links considered for comparison in our procedure. We observe that in our social networks, the percolation clusters close to the critical point are related to the community structure. This relationship is further highlighted by applying the procedure to model networks with predefined communities.

Physical Review E 83, 046112

Read the full text

M. Karsai, M. Kivelä, R. K. Pan, K. Kaski, J. Kertész, A.-L. Barabási, J. Saramäki

While communication networks show the small-world property of short paths, the spreading dynamics in them turns out slow. Here, the time evolution of information propagation is followed through communication networks by using empirical data on contact sequences and the susceptible-infected model. Introducing null models where event sequences are appropriately shuffled, we are able to distinguish between the contributions of different impeding effects. The slowing down of spreading is found to be caused mainly by weight-topology correlations and the bursty activity patterns of individuals.

Physical Review E 83, 025102(R)

Read the full text

A. Lancichinetti, M. Kivelä, J. Saramäki, S. Fortunato

Community structure is one of the key properties of complex networks and plays a crucial role in their topology and function. While an impressive amount of work has been done on the issue of community detection, very little attention has been so far devoted to the investigation of communities in real networks. We present a systematic empirical analysis of the statistical properties of communities in large information, communication, technological, biological, and social networks. We find that the mesoscopic organization of networks of the same category is remarkably similar. This is reflected in several characteristics of community structure, which can be used as “fingerprints” of specific network categories. While community size distributions are always broad, certain categories of networks consist mainly of tree-like communities, while others have denser modules. Average path lengths within communities initially grow logarithmically with community size, but the growth saturates or slows down for communities larger than a characteristic size. This behaviour is related to the presence of hubs within communities, whose roles differ across categories. Also the community embeddedness of nodes, measured in terms of the fraction of links within their communities, has a characteristic distribution for each category. Our findings are verified by the use of two fundamentally different community detection methods.

PloS ONE 5 (8), e11976

Read the full text

R. Toivonen, L. Kovanen, M. Kivelä, J.-P. Onnela, J. Saramäki, K. Kaski

This paper reviews, classifies and compares recent models for social networks that have mainly been published within the physics-oriented complex networks literature. The models fall into two categories: those in which the addition of new links is dependent on the (typically local) network structure (network evolution models, NEMs), and those in which links are generated based only on nodal attributes (nodal attribute models, NAMs). An exponential random graph model (ERGM) with structural dependencies is included for comparison. We fit models from each of these categories to two empirical acquaintance networks with respect to basic network properties. We compare higher order structures in the resulting networks with those in the data, with the aim of determining which models produce the most realistic network structure with respect to degree distributions, assortativity, clustering spectra, geodesic path distributions, and community structure (subgroups with dense internal connections). We find that the nodal attribute models successfully produce assortative networks and very clear community structure. However, they generate unrealistic clustering spectra and peaked degree distributions that do not match empirical data on large social networks. On the other hand, many of the network evolution models produce degree distributions and clustering spectra that agree more closely with data. They also generate assortative networks and community structure, although often not to the same extent as in the data. The ERGM model, which turned out to be near-degenerate in the parameter region best fitting our data, produces the weakest community structure.

Social Networks 31(4), p. 240–254

Read the full text