Tag Archives: networks

M Kivelä, J Cambe, J Saramäki, M Karsai

The dynamics of diffusion-like processes on temporal networks are influenced by correlations in the times of contacts. This influence is particularly strong for processes where the spreading agent has a limited lifetime at nodes: disease spreading (recovery time), diffusion of rumors (lifetime of information), and passenger routing (maximum acceptable time between transfers). We introduce weighted event graphs as a powerful and fast framework for studying connectivity determined by time-respecting paths where the allowed waiting times between contacts have an upper limit. We study percolation on the weighted event graphs and in the underlying temporal networks, with simulated and real-world networks. We show that this type of temporal-network percolation is analogous to directed percolation, and that it can be characterized by multiple order parameters.

Read the full text

D Hric, K Kaski, M Kivelä

In this study we map out the large-scale structure of citation networks of science journals and follow their evolution in time by using stochastic block models (SBMs). The SBM fitting procedures are principled methods that can be used to find hierarchical grouping of journals that show similar incoming and outgoing citations patterns. These methods work directly on the citation network without the need to construct auxiliary networks based on similarity of nodes. We fit the SBMs to the networks of journals we have constructed from the data set of around 630 million citations and find a variety of different types of groups, such as communities, bridges, sources, and sinks. In addition we use a recent generalization of SBMs to determine how much a manually curated classification of journals into subfields of science is related to the group structure of the journal network and how this relationship changes in time. The SBM method tries to find a network of blocks that is the best high-level representation of the network of journals, and we illustrate how these block networks (at various levels of resolution) can be used as maps of science.

Read the full text

M. Kivelä, M. A. Porter

We extend the concept of graph isomorphisms to multilayer networks with any number of “aspects” (i.e., types of layering), and we identify multiple types of isomorphisms. For example, in multilayer networks with a single aspect, permuting vertex labels, layer labels, and both vertex labels and layer labels each yield different isomorphism relations between multilayer networks. Multilayer network isomorphisms lead naturally to defining isomorphisms in any of the numerous types of network that can be represented as a multilayer network, and we thereby obtain isomorphisms for multiplex networks, temporal networks, networks with both of these features, and more. We reduce each of the multilayer network isomorphism problems to a graph isomorphism problem such that the size of the graph isomorphism problem grows linearly with the size of the multilayer network isomorphism problem. One can thus use software that has been developed to solve graph isomorphism problems as a practical means for solving multilayer network isomorphism problems. Our theory lays a foundation for extending many network analysis methods such as motifs, graphlets, structural roles, and network alignment to any multilayer network.

Read the full text

M. Kivelä, M. A. Porter

A diverse variety of processes — including recurrent disease episodes, neuron firing, and communication patterns among humans — can be described using inter-event time (IET) distributions. Many such processes are ongoing, although event sequences are only available during a finite observation window. Because the observation time window is more likely to begin or end during long IETs than during short ones, the analysis of such data is susceptible to a bias induced by the finite observation period. In this paper, we illustrate how this length bias is born and how it can be corrected without assuming any particular shape for the IET distribution. To do this, we model event sequences using stationary renewal processes, and we formulate simple heuristics for determining the severity of the bias. To illustrate our results, we focus on the example of empirical communication networks, which are temporal networks that are constructed from communication events. The IET distributions of such systems guide efforts to build models of human behavior, and the variance of IETs is very important for estimating the spreading rate of information in networks of temporal interactions. We analyze several well-known data sets from the literature, and we find that the resulting bias can lead to systematic underestimates of the variance in the IET distributions and that correcting for the bias can lead to qualitatively different results for the tails of the IET distributions.

Physical Review E 92 052813

Read the full text

E. Cozzo, M. Kivelä, M. De Domenico, A. Solé-Ribalta, A. Arenas, S. Gómez, M. A. Porter, Y. Moreno

Recent advances in the study of networked systems have highlighted that our interconnected world is composed of networks that are coupled to each other through different ‘layers’ that each represent one of many possible subsystems or types of interactions. Nevertheless, it is traditional to aggregate multilayer networks into a single weighted network in order to take advantage of existing tools. This is admittedly convenient, but it is also extremely problematic, as important information can be lost as a result. It is therefore important to develop multilayer generalizations of network concepts. In this paper, we analyze triadic relations and generalize the idea of transitivity to multiplex networks. By focusing on triadic relations, which yield the simplest type of transitivity, we generalize the concept and computation of clustering coefficients to multiplex networks. We show how the layered structure of such networks introduces a new degree of freedom that has a fundamental effect on transitivity. We compute multiplex clustering coefficients for several real multiplex networks and illustrate why one must take great care when generalizing standard network concepts to multiplex networks. We also derive analytical expressions for our clustering coefficients for ensemble averages of networks in a family of random multiplex networks. Our analysis illustrates that social networks have a strong tendency to promote redundancy by closing triads at every layer and that they thereby have a different type of multiplex transitivity from transportation networks, which do not exhibit such a tendency. These insights are invisible if one only studies aggregated networks.

New Journal of Physics 17(7), 073029

Read the full text

M. Kivelä, S. Arnaud-Haond, J. Saramäki

The recent application of graph-based network theory analysis to biogeography, community ecology and population genetics has created a need for user-friendly software, which would allow a wider accessibility to and adaptation of these methods. EDENetworks aims to fill this void by providing an easy-to-use interface for the whole analysis pipeline of ecological and evolutionary networks starting from matrices of species distributions, genotypes, bacterial OTUs or populations characterized genetically. The user can choose between several different ecological distance metrics, such as Bray-Curtis or Sorensen distance, or population genetic metrics such as FST or Goldstein distances, to turn the raw data into a distance/dissimilarity matrix. This matrix is then transformed into a network by manual or automatic thresholding based on percolation theory or by building the minimum spanning tree. The networks can be visualized along with auxiliary data and analysed with various metrics such as degree, clustering coefficient, assortativity and betweenness centrality. The statistical significance of the results can be estimated either by resampling the original biological data or by null models based on permutations of the data.

Molecular Ecology Resources 15(1) p. 117–122

Read the full text

The related software

M. Kivelä, A. Arenas, M. Barthelemy, J. P. Gleeson, Y. Moreno, M. A. Porter

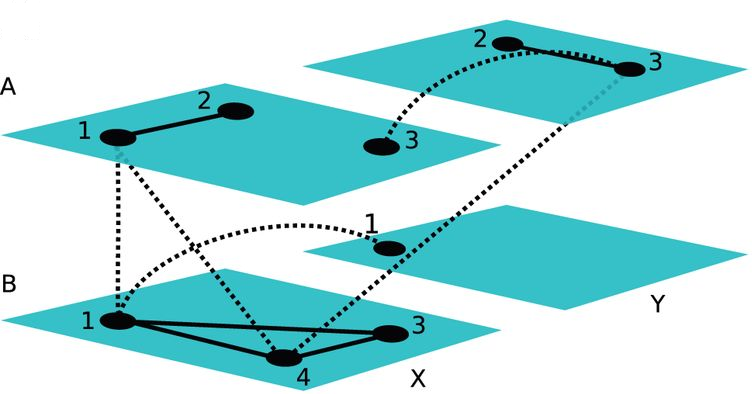
In most natural and engineered systems, a set of entities interact with each other in complicated patterns that can encompass multiple types of relationships, change in time and include other types of complications. Such systems include multiple subsystems and layers of connectivity, and it is important to take such ‘multilayer’ features into account to try to improve our understanding of complex systems. Consequently, it is necessary to generalize ‘traditional’ network theory by developing (and validating) a framework and associated tools to study multilayer systems in a comprehensive fashion. The origins of such efforts date back several decades and arose in multiple disciplines, and now the study of multilayer networks has become one of the most important directions in network science. In this paper, we discuss the history of multilayer networks (and related concepts) and review the exploding body of work on such networks. To unify the disparate terminology in the large body of recent work, we discuss a general framework for multilayer networks, construct a dictionary of terminology to relate the numerous existing concepts to each other and provide a thorough discussion that compares, contrasts and translates between related notions such as multilayer networks, multiplex networks, interdependent networks, networks of networks and many others. We also survey and discuss existing data sets that can be represented as multilayer networks. We review attempts to generalize single-layer-network diagnostics to multilayer networks. We also discuss the rapidly expanding research on multilayer-network models and notions like community structure, connected components, tensor decompositions and various types of dynamical processes on multilayer networks. We conclude with a summary and an outlook.

Journal of Complex Networks 2(3), p. 203-271

Read the full text

M. De Domenico, A. Solé-Ribalta, E. Cozzo, M. Kivelä, Y. Moreno, M. A. Porter, S. Gómez, A. Arenas

A network representation is useful for describing the structure of a large variety of complex systems. However, most real and engineered systems have multiple subsystems and layers of connectivity, and the data produced by such systems are very rich. Achieving a deep understanding of such systems necessitates generalizing “traditional” network theory, and the newfound deluge of data now makes it possible to test increasingly general frameworks for the study of networks. In particular, although adjacency matrices are useful to describe traditional single-layer networks, such a representation is insufficient for the analysis and description of multiplex and time-dependent networks. One must therefore develop a more general mathematical framework to cope with the challenges posed by multilayer complex systems. In this paper, we introduce a tensorial framework to study multilayer networks, and we discuss the generalization of several important network descriptors and dynamical processes—including degree centrality, clustering coefficients, eigenvector centrality, modularity, von Neumann entropy, and diffusion—for this framework. We examine the impact of different choices in constructing these generalizations, and we illustrate how to obtain known results for the special cases of single-layer and multiplex networks. Our tensorial approach will be helpful for tackling pressing problems in multilayer complex systems, such as inferring who is influencing whom (and by which media) in multichannel social networks and developing routing techniques for multimodal transportation systems.

Phys. Rev. X 3, 041022

Read the full text

R. Toivonen, M. Kivelä, J. Saramäki, M. Viinikainen, M. Vanhatalo, M. Sams

The aim of this work was to study the similarity network and hierarchical clustering of Finnish emotion concepts. Native speakers of Finnish evaluated similarity between the 50 most frequently used Finnish words describing emotional experiences. We hypothesized that methods developed within network theory, such as identifying clusters and specific local network structures, can reveal structures that would be difficult to discover using traditional methods such as multidimensional scaling (MDS) and ordinary cluster analysis. The concepts divided into three main clusters, which can be described as negative, positive, and surprise. Negative and positive clusters divided further into meaningful sub-clusters, corresponding to those found in previous studies. Importantly, this method allowed the same concept to be a member in more than one cluster. Our results suggest that studying particular network structures that do not fit into a low-dimensional description can shed additional light on why subjects evaluate certain concepts as similar. To encourage the use of network methods in analyzing similarity data, we provide the analysis software for free use (http://www.becs.tkk.fi/similaritynets/).

PloS ONE 7(1): e28883

Read the full text

M. Kivelä, R. K. Pan, K. Kaski, J. Kertész, J. Saramäki, M. Karsai

In temporal networks, both the topology of the underlying network and the timings of interaction events can be crucial in determining how a dynamic process mediated by the network unfolds. We have explored the limiting case of the speed of spreading in the SI model, set up such that an event between an infectious and a susceptible individual always transmits the infection. The speed of this process sets an upper bound for the speed of any dynamic process that is mediated through the interaction events of the network. With the help of temporal networks derived from large-scale time-stamped data on mobile phone calls, we extend earlier results that indicate the slowing-down effects of burstiness and temporal inhomogeneities. In such networks, links are not permanently active, but dynamic processes are mediated by recurrent events taking place on the links at specific points in time. We perform a multiscale analysis and pinpoint the importance of the timings of event sequences on individual links, their correlations with neighboring sequences, and the temporal pathways taken by the network-scale spreading process. This is achieved by studying empirically and analytically different characteristic relay times of links, relevant to the respective scales, and a set of temporal reference models that allow for removing selected time-domain correlations one by one. Our analysis shows that for the spreading velocity, time-domain inhomogeneities are as important as the network topology, which indicates the need to take time-domain information into account when studying spreading dynamics. In particular, results for the different characteristic relay times underline the importance of the burstiness of individual links.

Journal of Statistical Mechanics P03005

Read the full text